�i�P�X�X�V�^�T�^�P�O�@����Ԃ�Ԋ��j�@�@�@

�@���N�́A�C�M���X�̎��������w�ҁA�i�E�i�E�g���\�����d�q�����Ă��炿�傤�ǕS�N�ɂȂ�܂��B�����̐��藧����T������Ȋw�̗��j�̒��ŁA���̔����͐V���Ȏ���̖��J����������o�����ł����B���̃V���[�Y�ł́A�g���\���̔����ɂ��Ȃ�ŁA���q��菬�����~�N���̐��E�ɓ��ݍ������w���A�~�N���̐��E�̖@���ɓ��B����܂ł́A��l�����I�قǂ̗��j���Љ�����Ǝv���܂��B�@�@
�d�q�����������܂ł́A�����������ŏ��̒P�ʂ͌��q�Ƃ������q�ł���A���q�͌��f�̎�ނɑΉ����Čy�����̂�d�����̂�����A�܂��A���q������ȏ㕪�����邱�Ƃ͕s�\�ł���A�ƍl�����Ă��܂����B���̕����̌��q�_�́A�d�q�̔����惊�S�N�قǑO�A�C�M���X�̉Ȋw�ҁA�h���g���ɂ���āA���w�����ɂ������镨���Ԃ̗ʓI�ȊW���A�����I�ɐ����ł���A�����Ƃ��P���ō����I�ȗ��_�Ƃ��Ċm�����ꂽ�̂ł����B
�@ �@�@
�@�@
�@�ꎵ���N�ɃC�^���[�̃{���^���d�r�����Ă���A�����Ɠd�C�̑��݂̊W�����w�̐V���Ȍ�������ƂȂ�A�ꔪ�O�O�N�ɂ̓C�M���X�̉��w�҂ł��蕨���w�҂ł���t�@���f�[�ɂ���āA�d�C��������镨���̗ʂƂ���ɕK�v�ȓd�C�ʂ̊Ԃɂ�����Ƃ������W������Ƃ����A�d�C�����̖@�����m������܂����B�ꔪ���ܔN�ɂȂ�ƁA�A�C�������h�̃X�g�[�j�[�́A���f�̓d�C�����ɕK�v�ȓd�C�ʂ���l���āA���f���q����ɂ͖�P�O-20�N�[�����̓d�C�ʂ��������邱�Ƃ��Z�o���A���߂āu�d�q�iElectron�j�̌Ăі���^���܂����B�������A����͗��q�Ƃ��Ă̓d�q���l�����̂ł͂Ȃ��A�܂��d�C�f�ʂ̊T�O��^������̂ł�����܂���ł����B�@�@�@
�@�g���\���͈ꔪ�ܘZ�N�A�}���`�F�X�^�[�̋ߍx�ɐ��܂�܂����B�\�l�Ń}���`�F�X�^�[��w�ɓ��w�A�H�w��Ȋw���w��ňꔪ���Z�N�ɃP���u���b�W��w�𑲋ƁA��n�n�l�N�ɓ���w�̃J���F���f�B�V���������̋����ƂȂ�A���h�Ȋ�b���������w�̋��_�����݂����̂ł��B
�@�ނ��d�q�����邱�ƂɂȂ����̂́A�A�ɐ��̌�������ł����B�A�ɐ��́A�ꔪ�܌ܔN���납��h�C�c�̃{����w�̋Z�p�ҁA�K�C�X���[���A����w�̕����w�҃v�����b�J�[�̋��߂ɉ����ĊJ�������^����d�Ƃ�����������甭������܂����B�K���X�ǂ̒��ɓd�ɂ����A���d���������Ȃ���Ǔ��̋�C��^��|���v�Ŕ����ƁA�ɂȂ����C�̂�ʂ��ĕ��d���N����A�C�̌��f���L�̐F�̌��i�v���Y����ʂ��ăX�y�N�g���ɕ������邱�Ƃ��ł���j����A�Ƃ��������ł��B����ɊǓ��̋�C�������ĕ��d�ǂ̋C����������ƁA�^����d�̌��͎キ�Ȃ�A�����Ɋǂ̃K���X�����ΐF�Ɍu�����܂��B���̗l�q�����������A�ɂ�������̂悤�Ȃ��̂����˂���A�K���X�ɓ������Ă���悤�Ɍ����邽�߁A���̕��ː����A�ɐ��ƌĂ̂ł��B�ꔪ�Z��N����܂łɂ̓v�����b�J�[��q�b�g���t��ɂ��A�A�ɐ��͌u����p�̂ق��ɁA���i���邱�ƁA���̂ɂ����������͉e�ɂȂ邱�ƁA���C�Ői�H���Ȃ����邱�ƂȂǂ����炩�ɂ���Ă��܂����B
�@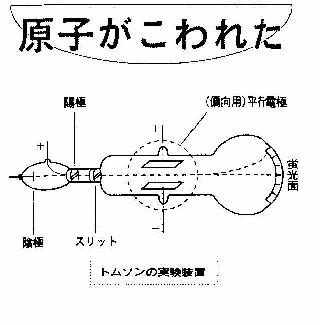
�g���\���͉A�ɐ��̐��̂����Ƃ߂�����������Ȃ����߂ɁA�^����d�ǂɉ��ǂ������܂����i�}�j�B�z�ɂɃX���b�g�i�ׂ������܁j���������ĉA�ɂ�����˂��������ׂ��r�[���Ƃ��ĊǓ���ʂ��A�r�[�����o�H�̓r���ŝp�ނ悤�Ɉ�̕��s�ȓd�ɂ�u���A���̓d�E�ɂ��r�[�����Ȃ�����悤�ɂ���A�r�[���̓�����K���X�ʂɌu��������h��A���̈ʒu�����₷������A�Ȃǂł��B����͍����̃u���E�����̌��^�ł��B
�@���s�d�ɂɓd����������ƁA�r�[���ɂ��u���ʂ̋P�_�����̕��s�d�ɂ̗z�ɂ̑��Ɉړ����܂��B���ɁA���s�d�ɂ̓d�ɖʂɕ��s�Ńs�[���ɐ����ȕ����Ɏ��E�������A���̋������������āA��Ɉڋ����P�_�����Ƃ̈ʒu�ɂ���悤�ɂ��Ă��܂��B�g���\���̓r�[�������ʂƓd�ׂ������������q�̗���ƍl���A���̂Ƃ��̓d�E�Ǝ��E�̋�������v�Z�����āA�����q�̎��ʂƓd�ׂ̔�����߂܂����B
�@�����N�A�h�C�c�̕����w�҃J�E�t�}�����A�ɐ��̗��q�̎��ʁE�d�ה�����߂܂������A���ʂ����[���l�@�����̂̓g���\���ł����B�ނ́A���d�ǒ��̋C�̂̎�ނ�A�ɂ̋����̎�ނ�ς��Ă��A��ɓ������ʁE�d�ה䂪�����邱�ƁA�܂��A�d���œ����鐅�f�́E���ʁE�d�ה�̒l����番�̈���������l�ł��邱�Ƃ���A���̗��q���}�C�i�X�̓d�ׂ������A�����Ƃ��y�����f���q���͂邩�ɏ������A�����錴�q�ɋ��ʂ������q�A�d�q�ł���ƍl�����̂ł��B
�@���̂��Ƃ́A�����錳�f�̌��q���A�d�q�Ƃ������ʂ̕��i�������Ƃ��Ӗ����A����܂ŕ����̋��ɂ̒P�ʂƍl�����Ă������q���A��菬�������i�ɕ����ł��邱�Ƃ��A�l�тƂɊm�M�����邱�ƂɂȂ����̂ł��B
�@�������āA�����̖{������������Ȋw�́A�V��������ɓ��݂��ނ��ƂɂȂ����̂ł��B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@�@���y�j�f��
�@�@�@
�i�P�X�X�V�^�T�^�P�V�@����Ԃ�Ԋ��j
�@�@�@
 �@�i�E�i�E�g���\�������������d�q�́A���̎��ʂƕ��̓d�ׂ������ĉ^����������q�ł����B�������ނ́A���ʂƓd�ׂ̔�����������̂́A���̎��͂��ꂻ��̒l��f��I�ɂ͎����܂���ł����B
�@�i�E�i�E�g���\�������������d�q�́A���̎��ʂƕ��̓d�ׂ������ĉ^����������q�ł����B�������ނ́A���ʂƓd�ׂ̔�����������̂́A���̎��͂��ꂻ��̒l��f��I�ɂ͎����܂���ł����B
�@�@�ꔪ���N�A�g���\���̓E�B���\���̘I���i�b�E�s�E�q�E�E�B���\���͋�C��c��������Ɩ����������邱�Ƃ𗘗p���Ė��������A����Z�N�ɂ͕��ː��̔�Ղ̂�����̐��Ƃ��Ċϑ��������ƂŗL���j���g���A�A�ɐ����q�͓d�C�����̍ۂ̐��f�C�I���Ɠ����ʂ̓d�C�������Ƃ��ؖ����A�ނ̓d�q�����̌��������������̂ł����B���������̒l�́A���x�̓_�Ŗ����̓����Ȃ����̂ł����B
�@�d�q�̓d�ׂ̐����Ȓl�������ɂ�莦�����̂́A�A�����J�̕����w�ҁA�g�E�`�E�~���J���i�ꔪ�Z���N�A�C���m�C�B���܂�j�ł����B
�@�ނ̓I�E�o�[�����E�J���b�W�ŏC�m�����Ƃ�A�R�����r�A��w�Ŕ��m�����l�����܂����i�ꔪ��ܔN�j�B���ŁA�x����������уQ�b�`���Q����w�Ŋw�сA�ꔪ��Z�N�ɃV�J�S��w�ɐE�܂����B
�@���Z���N�A�W�̓g���\����E�B���\���������Ȃ��Ă������H�ɕt������d�ׂ̌���������ɔ��W�����A���H�����R������������@�œd�q�̓d�ׂ𑪒肷��������n�߂܂����B�������A���H�ł͊ϑ����ɏ������đ傫�����ς���Ă��܂��A���m�Ȓl�������Ȃ����Ƃ��獪�{�I�ȉ��ǂ����킦�A���̓H�i���H�j���g�����Ƃɂ��܂����B
�@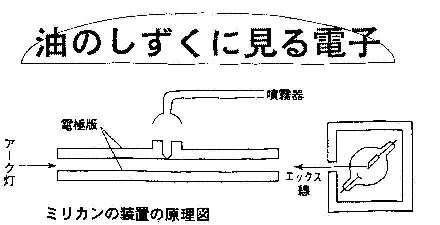
�@�~���J���̑��u�́A������ŎU�炵�Ē��a���~�N�����̖��H�����A�d�ɂ̏㕔�̏�����������d�ɂ̊Ԃɓ����܂��B�����w�G�b�N�X�����Ǝ˂��đѓd�����A�d�E��ω������āA���H�̗������x�̕ω����������Ŋϑ����Ė��H�̓d�ׂ𑪒肵�܂����B
�@����ꂽ�l�̂��ׂĂ��A����ŏ��P�ʗʂ̐����{�ɂȂ��Ă��邱�Ƃ���A���̒P�ʗʂ�f�d�ׁi�܂��͓d�C�f�ʁj�ƌĂсA�d�q������d�C�ʂƒ�߂܂����B
�@�~���J���͂���Ɉ���Z�N�ɂ����Ď������J��Ԃ��A�d�q�̓d�ׂƂ��āi1.590�}0.002�j��10-19�N�[�����܂����B�i���݂̒l��1.602�w10-19�N�[�����ŁA���̍���0.8���ɉ߂��Ȃ��j�B�f�d�ׂ̌���͂܂��A�d�q�̎��ʂ����f���q���͂邩�Ɍy���i���悻��番�́[�j���Ƃɂ��m�M�����������̂ł��B
�@�����ɁA���q����d�q�������������ɂ́A���̓d�ׂ�����A�����̎��ʂ̑唼���ɂȂ����������݂���͂��ł��邱�ƁA�Ȃǂ̐V���ȋ^�₪�����яオ�邱�ƂƂȂ����̂ł��B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@�@
�i�P�X�X�V�^�T�^�Q�S�@����Ԃ�Ԋ��j�@�@�@

�@�i�E�i�E�g���\���́A���̓d�ׂ͌��q���̏��������ł���d�q���S���Ă���̂ɂ������A���̓d�ׂ͌��q�S�̂ɕ��ς��ĂЂ낪���Ă���A�ƍl���܂����i�g���\���̌��q�͌^�A���Z�O�N�j�B�قړ�������A���{�̕����w�ҁA���������Y�̍l�����͌^�́A���d�ׂ����������̂̂܂��𑽐��̓d�q�������O��ɘA�Ȃ��ĉ�]���Ă���Ƃ������̂ł����i�y���^�͌^�j�B
�@�����̖͌^����Ă����ƁA������̖͌^���^�������߂����ĕ����w�҂̊ԂōL���c�_���N����A���_�I�ɂ������I�ɂ����܂��܂Ȏ��݂��W�J����܂��B���̒��̈�l�ɁA���ː��̌����͓I�ɐi�߂Ă����d�E���U�t�H�[�h������܂����B
�@���U�t�H�[�h�͈ꔪ����N�ɓ[�W�[�����h�Ő��܂�A���w���ŃJ���^�x���[�E�J���b�W�Ɋw��C�M���X�ɓn��A�P���u���b�W��w�E�L���x���f�B�b�V���������̌������ƂȂ�A�����Ńg���\���Ƃ̋��������ŁA�G�b�N�X�����C�̂�d�������Đ����̃C�I������邱�Ƃ\�i�ꔪ��Z�j���Ă��܂��B�ꔪ�㔪�N�A�����g���I�[���̃}�M����w�����A���Z���N�A�}���`�F�X�^�[��w�����A�����`�O���N�ɂ͂i�E�i�E�g���\���̌�C�Ƃ��ăL���x���f�B�c�V���������̏����߂܂����B
�@�ނ͈ꔪ���N�A���ː��ɂ͓��ߗ͂̈Ⴄ�A���t�@���ƃx�[�^��������Ɣ��\�A���Z���N�ɂ͎���ɂ��A���t�@�����Ȃ��邱�Ƃ���A���̐��̂͐��d�ׂ̏d���������q�ł��邱�ƁA���Z���N�ɂ̓A���t�@���i�A���t�@���q�j�̓w���E���̃C�I���ł��邱�Ƃ������ŗ�����ȂǁA���X�̌��������Ă��܂����B
�@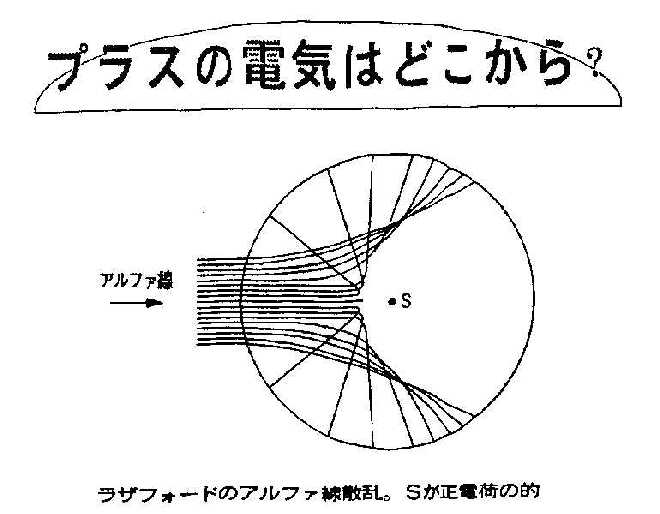
�@�ނ����ڂ����͈̂��Z��N�ɃK�C�K�[�ƃ}���X�f���������Ȃ����A���t�@���𔖂��A���~���i�͂��j�ɓ��Ă�����̌��ʂł����B�啔���̃A���t�@���q���g���\���̖͌^����\�z�����悤�ɏ������p�x�����i�H��ς��Ȃ��Ȃ��ŁA�\�z�ȏ�̐��̃A���t�@���q����Z�x�ȏ�̑傫���p�x�ŋȂ���̂ł��B���U�t�H�[�h�͎�X�̌��f�ɂ��Ă��A���t�@���̎����������Ȃ��A�܂��A�A���t�@���q�����̓d�ׂ����I�i�܂Ɓj�ɂ���ĎU�������l�q��\���v�Z�����A�������ʂƌv�Z���ʂ��Ƃ炵���킹�܂����B
�@���̌��ʁA���f�̌��q�ԍ��Ɠ��������̐��̑f�d�ׂ������A�����̓y���͌^�̐��d�����͂邩�ɏ������P�O-13�p���̌��q�j�i���q�͖�P�O-8�p�j�ƌĂԂׂ����q�̑��݂𗧏����̂ł��B
�@���q�͂���܂ōl�����Ă��������͂邩�ɏ��������q����Ȃ��Ă��āA�����͂����Ԃ��炯�ł���Ƃ����A�ӊO�ȕ������������яオ���Ă����̂ł��B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@���y�j�f��
�u�v���X�̓d�C�͂ǂ�����H�v�́u�ǂ��ɁH�v�ɒ���
�i�P�X�X�V�^�T�^�R�P�@����Ԃ�Ԋ��j�@�@�@

 �@
�@
�@�����ŁA�d�q�̘b���炻���Ǝv���邩������܂��A���̘b���Љ�Ă����܂��傤�B
�@��Ԃ�`���d���g�����݂��A�����d���g�̈��ł��낤�A�Ɨ��_�I�ɗ\�������̂́A�C�M���X�̕����w�҃}�N�X�E�[���ł����i�ꔪ�Z��j���̗\���͂P�W�W�W�N�Ƀh�C�c�̃w���c�ɂ������I�Ɋm�F����A���̗��q���͉e���Ђ��߂܂����B
�@�X�g�[�u�⑾�z�ȂǁA�����̕��̂����˂���M���������g���̒����d���g�ł��B�傫�ȓS����Ă����ꂷ��H��ł́A�傫�ȘF�ɓS������A���x���グ�Ă����܂��B�F���̉��x���Ď����邽�߂ɂ�������ꂽ�������̂��������猩�Ă���ƁA�ŏ��͐^���Âʼn��������܂��A���x���オ��ɏ]���ĈÂ��Ԃ̌��������A����ɖ��邢�ԁA���F�A���F�A�ƕς���Ă��܂��B�����ɔM�������o����܂��B
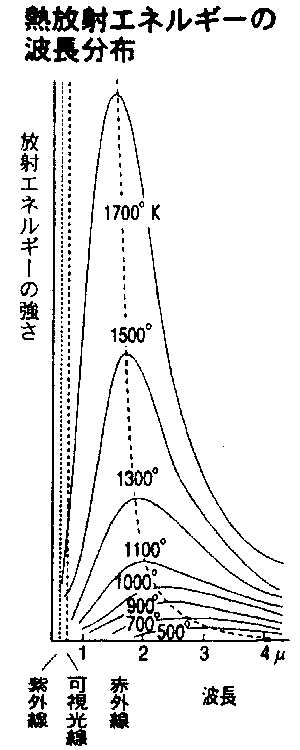
�@�����w�҂��������̌��ۂ��ϑ����A�F�̉��x���オ��ɂ�āA�F���̓d���g�i����M��j�̔g���Ƌ����̊W���A�O���t�̋Ȑ��̂悤�ɕς���Ă��邱�Ƃ��킩��܂����B
�@���̂悤�ȋȐ��i�g���A���x�A���x�A�̊��W�j�͂ǂ����Đ��藧���Ă���̂����A���܂łɒm���Ă��镨���@�������������̂����_�����w�̖����ł��B���C���[�ƃW�[���Y���l���������́A�g���������Ƃ��͂悭�����ƍ����A�g�����Z���Ƃ��̓E�B�[���̒�Ă����������悭�����܂����B���̔��ł͂�����̌������������炸��Ă��܂��܂��B
�@�h�C�c�̕����w�҂l�E�v�����N�́A������̌������q���g�Ƃ��āA�S�g���̈�Ŏ����Ƃ悭�������������A����ɂ��̌������Ӗ����镨���I�����ɂ��čl�@��[�߁A�H�l���M�[�ɂ���v���I�ȍl���ɓ��B�����̂ł��B����́A���ׂĂ̕��̂͂���ȏ㕪�����Ȃ����q���琬�藧���Ă���Ɠ����ɁA�G�l���M�[������Ȃ���������������悤�ȘA���ʂł͂Ȃ��A����f�ʁi�G�l���M�[�ʎq�j���琬�藧���Ă���A�Ƃ������̂ł��B���̍l���ɂ��ƂÂ��A�M���˂ɂ��闝�_�͊��������̂ł��i���Z�Z�j�B
�@
�@�v�����N�̍l���ɂ��ρA�G�l���M�[�ʎq�͓d���g�̐U�������傫���قǁi�g�����Z���قǁj�傫���̂ŁA�G�l���M�[�̕s�A�����ڗ����A�g���������Ƃ��͘A�����Ă���悤�Ɍ����邱�ƂɂȂ�܂��B�G�l���M�[�ʎq���傫���Ȃ���́A�ꓮ���闱�q�Ƃ��Ă̐����������ɂȂ�A���ʎq�i�t�H�g���j�ƌĂ�邱�ƂɂȂ�܂��i���Z�ܔN�A�A�C���V���^�C���̌��ʎq���j�B
�@���ɂ��邱���̍l���́A��ɓd�q�̋����ׂ����̂����鎅���ɂȂ�̂ł��B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@�@���y�j�f��
�i�P�X�X�V�^�U�^�V�@����Ԃ�Ԋ��j�@�@�@

�@���������A���ɂ���b�𑱂��܂��傤�B����́A���w�����̉��F�����A���邢�̓K�C�X���[�ǂɂ��K�X���d�Ō����錳�f�ɓ��L�ȐF�̌��ɂ��Ăł��B�����̌����A�X���b�g�ƌĂ��ׂ������Ԃ�ʂ��ăv���Y��������ȂǂŌ���ƁA���{���̔g���̈قȂ���̐��ɕ�����܂��B�����A�̔g���̑g�ݍ��킹�̓X�y�N�g���ƌĂ�A���f�̎�ނɓ��L�̃X�y�N�g���������Ƃ���A���q�X�y�N�g���Ƃ������܂��B
�@���̐��������p���āA�X�y�N�g�����ϑ����Ă��̕����Ɋ܂܂ꌳ�f�ׂ邱�Ƃ��ł��܂��B����́A�������͖@�Ƃ����A�h�C�c�̉��w�҂q�E�v�E�v���[���ɂ�肻�̊�b���m�����ꂽ�̂ł��i�ꔪ�Z�Z�j�B���̕��@�͐V���f�̔����ɂ��L�͂Ȏ�i�ŁA���Ȃ��N�Ƀv���[���̓Z�V�E���ƁA���N�ɂ̓��r�W�E�������Ă��܂��B
�@���q�X�y�N�g���͌��f�̎�ނɂ�肳�܂��܂ŁA�����̊ԂɋK�����������������Ƃ͍���ł����B�������A�ꔪ���ܔN�Ɏ����āA�����Ƃ��y�����f�̌��q�X�y�N�g���ɂ��āA�X�C�X�̒��w�Z�̋��t�ł���p���}�[���ŏ��ɃX�y�N�g���n��̌����������̂ł��B�ނ́A�g���̒���������l�Ԗڂ̃X�y�N�g���܂ł̔g�������ꂼ��A����g�� h(=3645.6�~10-8�p)��9/5,16/12,25/21,36/32�{�ɂȂ��Ă��邱�Ƃ���A�����̕������An2/(n2-4),������n��3,4,5,6�Ƒ��������A�ł���Ɖ�ǂ����̂ł��B�������ނ́A���f�ȊO�̌��q�X�y�N�g���ɂ��Ă̋K�����͔����ł��܂���ł����B
�@
�@���̓��̓������������̂̓X�E�F�[�f���̕����w�ҁA�i�E�q�E�����[�h�x���ł����B�ނ́A�o���}�[�̌��������~���ɂ��A���̌��q�X�y�N�g���ɂ����Ă͂܂�K���i�����j�������邽�߁A�X�y�N�g��������A���A�s�i=P,D,S�j�̂R�n��ɕ����A���ꂼ��̌n��ɋ��ʂ��������i�����[�h�x���̌����j�ƁA���ׂĂ̌n��ɋ��ʂ̕��Ւ萔�i�����[�h�x���萔���o�i�ꔪ��Z�j���A�܂��A�قȂ�n��Ԃ̊W���l�Ղ��A�����@�[�h�x���]�V���[�X�^�[�̋K�����o���܂����i�ꔪ��Z�j�B
�@�@�����[�h�x���ɂ��K���́[�ʉ��͐��f���q�X�y�N�g���̃o���}�[�̌n��̎��O�����ɂ��A�ԊO�����ɂ��A����ɑ����̌n���邱�Ƃ�\�z�����A��������܂����B�����́A�����҂̖��O�ŌĂ͂�A�g���̒Z���i�G�l���M�[�̍����j���ɁA���C�}���n��A�n���}�[�n��A�p�b�V�F���n��A�v���b�P�b�g�n��A�ƌĂ�܂��B
�@�@����猴�q�X�y�N�g���̋K�������A1,2,3,����Ƃ����������܂ސ���ŕ\���ł��邱�Ƃ́A�O��̃G�l���M�[�ʎq�ƍl�����킹�āA���q�����̃G�l���M�[���A�����������ɂ����ׂ���ƂтƂт̒l�����Ƃ�Ȃ����Ƃ��Î����Ă���̂ł��B
�@�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@���y�j�f��
�i�P�X�X�V�^�U�^�P�S�@����Ԃ�Ԋ��j�@�@�@

�@���āA�i�E�i�E�g���\���ɂ��d�q�̔����Ƃd�E���U�t�H�[�h�ɂ�錴�q�j�̔����́A�������Ȃ킿���q�͓d�q�ƌ��q�j�őg�ݗ��Ă��Ă���ɈႢ�Ȃ��A�Ƃ̍l����l�тƂɂ������܂����B�ł��ȒP�Ȑ��f���q�́A���ꂼ�ꐳ�ƕ��̑f�d�ׂ����������q�j�Ɠd�q�̑ŁA�y���d�q�͏d�����q�j�̂܂����A���q�j�̐��d�ׂ̈��͂��Ȃ���~�^�����Ă���A�ƍl���܂��B���傤�ǁA���z�̂܂������]����f���̏ꍇ�̂悤�ɁA�[�g���J�w���g���ēd�q�̋O�����a�Ɖ�]�����̊W���v�Z����܂��B
�@�������A���ꂾ���ł͋O�����a�͒�܂炸�A���f���q�̑傫���͂܂��܂��ɂȂ��Ă��܂��܂��B�Ȃɂ��A���a�����߂����������͂��ł��B
�@�Ƃ��낪�A���̑��z�n���f���ɂ͂��������������܂����B�}�N�X�E�F���̓d�����_�ɂ��A���q�j�̂܂�����]����d�q�̓G�l���M�[��d���g�̌`�ŕ��o���Ď����A�₪�Č��q�j�ɗ�������ł��܂��͂��Ȃ̂ł��B�����Ȃ�A���ׂĂ̕����͓d�C�����������q�j��������ł��Ă��邱�ƂɂȂ�A���U�t�H�[�h�̔����Ɩ������܂��B
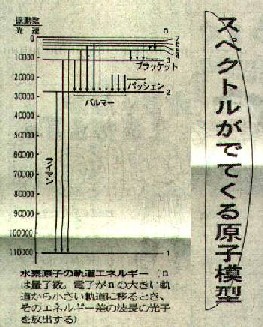
�@���̖��������������_�ȍl���������Č��q�͌^��g�ݗ��Ă��̂̓f���}�[�N�̕����w��N�E�{�[�A�i�[�n�n�܁`���Z��j�ł����B�ނ́A�d�q�̊p�^���ʂ́A����l�i�p�^���i�f�ʁ�1.055�~10-34�E�b�j�̐����{�����Ƃ蓾�Ȃ��A�Ɖ��肵�ēd�q�̋O�����a�ƍH�l���M�[���v�Z�����̂ł��B����Ƃ��Ԗڂ̋O�����a�́i0.529�~10-10�jn2(m)�j�ƂȂ�܂����B�����Ƃ��������O���͂���1�̏ꍇ�ł�����A���ʓ��̐��l�ŁA�u�{�[�A���a�v�Ƃ����A�قڌ��q�̑傫���ɂȂ�܂��B�܂��A�d�q�̃G�l���M�[�́i-2.18�~10-18�j/��2�i�W���[���j�ŕ\����A���ʓ��̒l��n=1�̋O���ɂ���Ƃ��̍Œ�G�l���M�[��Ԃł��B�O����G�l���M�[�̏��Ԃ�\�������u�ʎq���v�ƌĂт܂��B
�@�@�d�q�����Ԗڂ������H�l���M�[��Ԃ��炎�Ԗڂ̒Ⴂ��ԂɈڂ�Ƃ��A���̃G�l���M�[�̍��ɑ���������q����o����Ƃ��Ĕg�����v�Z����ƁA���[�g���ŁA�i9.12�~10-10�j�En2n'2/�in2-n'2�j�ƌv�Z����܂��B������n'=2�Ƃ��Ă���3�E4�E5�E6�Ə��Ԃɕς��Ĕg�������߂���A�Ȃ�ƁA�����Ŋϑ�����鐅�f���q�X�y�N�g���̃o���}�[�n��ƈ�v����ł͂���܂��B������肩�An'��1�E3�E4�Ƃ���ƁA���C�}���A�p�b�V�F���A�u���b�P�b�g�̌n����S���łĂ����̂ł��B
�@�@���q�̃{�[�A�͌^�����\�����i�P�X�P�R�j��A���E�̕����w�҂����������ɒ��ڂ��A���ꂼ�ꎩ�����Ђ������Ă̑�c�_���W�J����邱�ƂɂȂ�܂��B�����āA�R�y���n�[�Q����w�́@�㊥��\���̃{�[�A�̂��߂ɁA���_�����w�����̃|�X�g��p�ӂ����̂ł����i�A�C�͈��O���N�j�B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j���y�j�f��
�i�P�X�X�V�^�U�^�Q�P�@����Ԃ�Ԋ��j�@�@�@

�@�{�[�A�̌��q�͌^�����f���q�̃X�y�N�g���n����ς悭�������Ă��邱�Ƃ͂ƂĂ����R�Ƃ͎v���܂���B�{�[�A���͌^��g�ݗ��Ă�O��Ƃ����u�p�^���f�ʂ̐����{�̋O���������������v�Ƃ��������i�{�[�A�̗ʎq�����j�́A�Ȃɂ������Ƃ��ȍ���������Ǝv���܂��B���������������ƂɁA���̗ʎq�����́A���łɂ��̐��������\���Ɏ�����Ă���}�b�N�X�E�F���̓d�����_�Ƒ�����Ȃ��̂ł��@�i�O��Q�Ɓj�B

�@���̓��ɂ������āA�����ɂ���܂������V�����l�������邱�Ƃɂ������̓����J�����̂́A�t�����X�̕����w�ҁA�h�E�u���C�i�ꔪ���`��㔪���j�ł����i����O�j�B���q�̉^���ł́A���������ʂȈӖ��������Ƃ͂߂����ɂ���܂��A�g���ł͂����ΐ���������܂��B���Ƃ��A����e�����Ƃ��̐U���͊�{���g���Ƃ��̐����{�̐U���Ƃ��d�Ȃ��Ă�����̂ł��B�h�E�u���C�́A�{�[�A�̗��_�ɐ����������̂́A�d�q���g���g���̐����������Ă��邩��ł͂Ȃ����A�ƍl�����̂ł��B
�@�i�E�i�E�g���\���̎����ł��m�E�{�[�A�̖͌^�ł��A�d�q�͉^�����闱�q�Ƃ��Čv�Z����Ă��܂����B��������߂Ĕg�Ƃ��čl�������̂ł�����A�h�E�u���C�̔��z�͓��˂Ǝv���l������ł��傤�B�������A���̔��z�ɂ̓A�C���V���^�C���̌��ʎq���i���Z�܁j�Ƃ������~�����������̂ł��B

�@���͉�܂⊱�Ƃ����g���Ɠ��̌��ۂ������邱�Ƃ���g�ƍl�����܂������A�����������̓d�q���O�ւ͂����Ƃ����d���ʂ�G�b�N�X�����d�q�ƏՓ˂�����ɁA�d�q�ɗ^�����H�l���M�[�̕������G�l���M�[���������Ȃ�R���v�g�����ʂȂǂ́A�������̐U�����ɔ�Ⴕ���G�l���M�[�������ĉ^�����闱�q�i���ʎq�j�Ƃ��ď��߂Đ��������̂ł��B
�@���Ȃ킿�A���́A���鎞�͔g�Ƃ��ĐU�镑���A�܂�����Ƃ��͗��q�Ƃ��ĐU�镑���Ƃ�����d���i�҂Ȃ̂ł��B�h�E�u���C�͗��q�Ɣg�̓�d���i���������łȂ��A�d�q�̂悤�ȕ������\�����闱�q�ɂ܂Ŋg�������̂ł��i���̔g�̓h�E�u���C�g�A�܂��͕����g�Ƃ����܂��j�B
�@�h�E�u���C�́A����̒����������g�̔g���̐����{�ɂȂ��Ă���O���������������A�Ƃ���ƃ{�[�A�̗ʎq�������ȒP�ɂłĂ��邱�Ƃ������܂����B
�@���̌�A�A�ɐ����������i�͂��j�ɓ��Ă�ƁA���傤�ǍH�b�N�X���Ă��Ƃ��̂悤�ȉ�ܑ��������邱�Ƃ���A�d�q�͌��q�O�̎��R��Ԃł��g���ł��邱�Ƃ��m���߂��A�����g�͎����I�ɂ��m�F���ꂽ�̂ł��B
�@�@�i����G�E�֓��w�@��w�u�t�������w�j���y�j�f��
�i�P�X�X�V�^�U�^�Q�W�@����Ԃ�Ԋ��j�@�@�@

�@�m�E�{�[�A�̌��q�͌^�����f���q�X�y�N�g���̐����ɐ�������ƁA���f�ȊO�̌��q�ɂ��Ă��d�q�̋O���ƃX�y�N�g���̊W�̖Ȗ��Ȍ����������Ȃ���悤�ɂȂ�܂����B���̌��ʁA�������\�̏�ł̌��q���̓d�q�̔z�u�̗l�q������ɖ��炩�ɂ���܂����B
�@�����̌������Ƃ��ɒ��Ӑ[���l�@�����̂́A�I�[�X�g���A�̕����w�҂v�E�p�E���ł����B�ނ́A���q��g�ݗ��Ă�d�q���A�ǂ̂悤�ȋK���ɂ��ƂÂ��ċO����̐Ȃ��߂Ă���������������̂ł��B
�@�܂��A��̌��q���̓d�q�͎l�̗ʎq���œ����Â����܂��B
�@���́A��ʎq���Ƃ����A����n�ŕ\���܂��B����́A�O���̃G�l���M�[���ʂ�\�����̂ł��Bn=1,2,3,4�E�E�ɑΉ����ċO���͌��q�j�𒆐S�Ƃ��ē������珇�ɑw��ɂƂ�܂��܂��B������d�q�k�Ƃ����܂��B��������j�k�A�k�v�A�l�v�A�m�k�A����Ƃ�т܂��B
�@��Q�́A���ʗʎq���Ƃ����A�������ŕ\���܂��B��ʎq�����̋O���ɂ͂�=0,1,���,�in-1�j�Ƃ����ʎq��������܂��B�����͋O���ʂ̕������������̂ŁA���O���A���O���A���O���A���O���A�ȂǂƌĂ�܂��B
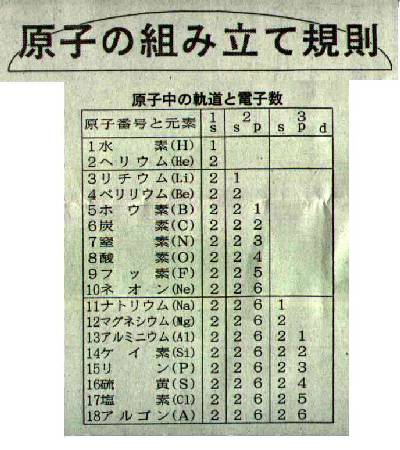
�@��R�́A���C�ʎq���ŁA�������ŕ\���܂��B���ʗʎq�����ɂ������Ă�=-��,-(��-1�j,���,-1,0,+1����+(��-1�j,+���́A�S���Łi2��+1�j�̗ʎq������Ȃ��Ă��܂��B
�@��l�́A�X�s���ʎq���Ƃ����A���ŕ\���܂��B���ɂ́{1/2,-1/2�̓��������܂���B

�@�p�E���́A���A���A���Œ�܂��̋O���ɂ́A�������ꂼ�ꐳ�ƕ��̓�̓d�q�܂ł�������Ȃ��A�Ƃ����K�����Ă��܂����i�P�X�Q�T�j�B������p�E���̌����ƌĂт܂��B���̋K���ɏ]���Đ��f���q����������\�̏��ɓd�q�Ă͂߂Ă݂܂��傤�B���q�ԍ��P�Ԃ̐��f�͂����P�̂r�O���Ɉ�̓d�q�����邾���ł��B�Q�Ԃ̃w���E���́A�����O���ɁA�r�̐��ƕ��̓d�q�Q�����܂��B�����Q�̂k�k�͂�=0,1���Ȃ킿���A���A�Q�̋O��������A���O���ɂ͂Q�A���O���͂���ɂ���-1,0,+1�̎O�̋O���ɕ������̂ŘZ�A���v���̓d�q������邱�ƂɂȂ�܂��B������ɓ���Ă����ƁA���q�_���R�Ԃ̃��`�E������P�O�Ԃ̃l�I���܂ł����т܂��B���̂悤�ɏ��Ɋk�߂Ă����ƁA���傤�ǎ������\�̋K���ɏ]�����d�q�̔z�u���ł���̂ł��B
�@�d�q�̏�Ԃ����������l�̗ʎq���́A���܂��܂Ȍ��q�X�y�N�g�����������\�ƑΏƂ��Ȃ��番�͂��A����ꂽ���ʂ������̂ł��B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@�@���y�j�f��
�i�P�X�X�V�^�V�^�T�@����Ԃ�Ԋ��j�@�@�@

�@�l�̗ʎq���ƃp�E���̌����Ŏ������\�ɑΉ������d�q�̔z�u�͌����ɐ�������܂����B��ʎq���̓{�[�A�̌��q�͌^�ŏ��߂Ĉďo���ꂽ�̂ł����A���̂R�̗ʎq�����A�X�y�N�g���ƋO���J�ڂ��A�d��⎥��̉e���Ȃǂ��������Ă��ڂ����l�@���ē���ꂽ�̂ł���A�����l���̉����ł���Ƃ����܂��B

�@�����ۂ��A�d�q�͕����g�ł���Ƃ���h�E�u���C�̉����́A�ʎq���i�G�l���M�[��^���ʂɐ���������邱�Ɓj���悭�������܂��B
�@�������A���鎞�͗��q�ŕʂ̎��͔g�A�ȂǂƂ������̂͂ƂĂ��l���ɂ������Ƃł����B�Ȃ��ɂ́A�����w�I���R�������傹��͔]�ɉf�������ƍl����l������܂����B
�@���̂悤�ȂȂ��ŁA�h�C�c�̕����w�҂d�E�V�����[�f�B���K�[�i�ꔪ�����`���Z��j�́A�h�E�v���C�̕����g�Ɨ��q���Ƃ̓����O��I�ɍl�@���A��̊�b���������o�����̂ł��i����Z�j�B����́u�V�����[�f�B���K�[�̔g���������v�ƌĂ�A����ɂ��ƂÂ����_���g���͊w�Ƃ����܂��B���̗��_�ɂ��ƁA���A���A���̂R�̗ʎq�����������̉��Ƃ��ďo�Ă��i�S�ڂ̗ʎq�����͈���n�N�̂l�E�f�B���c�N�ɂ��������̑��Θ_����ꂽ���ǂɂ��o�Ă���j�A�d��E����̉e�����ł̃X�y�N�g���ϑ��Ƃ��悭��v����̂ł��B

�@�g���͊w����o�����O�̔N�A�h�C�c�̕����w�҂v�E�n�C�[���x���N�i���Z��`��㎵�Z�j�̓{�[�A�̗ʎq�_�W�������s��͊w�Ƃ������̂��o���܂����B���̗��_�ł͔g���ɂ��Ă͍l������Ă��Ȃ��̂ł����A���̌��ʂ͔g���͊w�Ɗ�Ɉ�v����̂ł��B�V�����[�f�B���K�[�͈�v�̗��R�ɂ��Ă��l�@���A�Ƃ��Ƃ�������̗��_�͂܂����������Ȃ��̂ł��邱�Ƃ��ؖ����Ă��܂����̂ł��i����Z�j�B�������ʎq�͊w�����܂ꂽ�̂ł����B
�@�ʎq�͊w�ł͔g�̐U���̂Q��͗��q�̑��݊m����\���Ɖ��߂���܂��B��̐��f���q�̓d�q���u�Ԃ��Ƃɂǂ��ɂ��邩�͋C�܂���ł����A������ϑ�����ƁA�_���x�̔Z�W�Ƃ��ċO���̌`���`�����̂ł��B
�@�ʎq�͊w�́A�d�q�ȊO�̃~�N���ȗ��q�ɂ����Ă͂܂�܂��B�����w�͂��ɁA����܂Œʗp���Ă����}�N�����E�̕����w�Ƃ͈قȂ�A�~�N�����E�̉^���@���̗��_�̌n���\�z���邱�ƂɂȂ����̂ł��B
�@�����҂��Ă��������B�}�N���ȕ������~�N���ȕ����̏W���ł��ˁB����Ȃ̂ɂȂ��]���@�����Ⴄ�̂ł��傤�B
�@����A�^��Ɏv����_�A�����Ƃ��ł��B����͂��̐��������Ȃ���Ȃ�܂���B
�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@���y�j�A��
�i�P�X�X�V�^�V�^�P�Q�@����Ԃ�Ԋ��j�@�@�@

�@�킽�����������ڊ��m�ł��鎩�R�E�́A�قƂ�ǂ������Ƃ����Ă悢�قǑ����̌��q����Ȃ镨�̂ƁA���̕��̂����Z���^������L���̋�Ԃ��琬���Ă��܂��B�Ȋw�I�ϑ�������ƁA�����ۂ̈��ʊW���l�@�����_�Ƃ̌𗬂�ʂ����Ȋw�̔��W�́A�킽�������l�Ԃ̎��R�F���\�͂����I�Ɋg�債�Ă����܂����B
�@���z�n�̘f���Ԃɐ��藧�P�v���[�̖@�����疜�L���͂̑��݂��ؖ�����A�d�C�E���C�̕s�v�c�Ȍ��ۂ��n���I�Ɏ��������t�@���f�[�̓d���C�w���}�b�N�X�E�F�������_�I�Ɍ������āA�d���g�̑��݂�\�����A����ɁA�M�̖{���q�E���q�E�d�q�Ȃǂ̗��q�̉^���Ɠd���g�̃G�l���M�[�ƌ��邱�Ƃ��ł����̂��A�F���͈͂̊g��������Ă��܂��B
�@�i�E�i�E�g���\���ɂ��d�q�̔�������ʎq�͊w�̐����܂ł̕����w�̔��W�́A�킽�������̐��E���ɒ[�ɏ������~�N���̐��E�ɂ܂ŔF���͈͂��g�債�A�����Ő��藧�����@�����}�N�����E�̂��̂ƈႤ���Ƃ��������̂ł��B
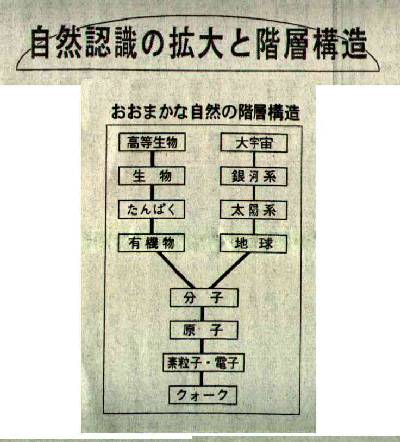
�@����A�~�N���̕�����ςݏd�˂ă}�N���̕����̐��E������̂ŁA�������܂������ʂ̐��E�ƍl����킯�ɂ͂����܂���B�����ŁA���R�͈������ǂ��A���̃X�P�[���i�T�C�Y�Ɍ���Ȃ��j�̈Ⴂ�ɂ�肢�����̊K�w�ɕ�����Ă���ƌ��܂��B������u���R�̊K�w�\���v�ƌĂт܂��B
�@�Ƃ��낪�A��ϓs�����悢���ƂɁA�~�N���̊K�w�̕����@���A�ʎq�͊w�́A��萔�̑����~�N���ȕ����̏W���̂ɓ��Ă͂߂Ă����ƁA����Ƀ}�N�����E�̕����@���A�ÓT�����w�ɋ߂Â��Ƃ����`�ɂȂ��Ă���̂ł��B��������̂͂��A�ʎq�͊w�̊J�ю҂����́A�ʎq�_�́A�@���͈قȂ��Ă��Ă��A�ÓT�����w�ɑΉ����闝�_�\�������ׂ����A�ƍl���Č�����������ł��B
�@��\���I���I��낤�Ƃ��錻��̉Ȋw�́A���R�E��S�ʓI�ɉ𖾂��悤�Ƃ��Ă��܂��B���̂�����܂��ȊK�w�\���͐}�̂悤�ł���Ƃ݂��܂��B
�@�����w�́A����ɐV���ȗ��_���\�z���A�f���q�̂���ɉ��̊K�w�A�N�H�[�N�̐��E�����܂����B�܂��~�N���̕����w���g���āA����ȉF���̊K�w�\�������炩���ɂ���܂����B��̊K�w�ɂ��A���Ƃ��ΐ����̂悤�ɁA����ɑ����̊K�w�\�������邱�Ƃ��킩��܂��A�����̊K�w�ɂ͂��ꂼ��Ǝ��̖@��������A�����������̖@���́A�݂��ɈقȂ��Ă͂��邪�������邱�ƂȂ��A�אڂ���K�w�̖@���̊Ԃł͑Ή��W�����藧���Ă���Ƃ݂��܂��B
�@�d�q��������S�N�B�Q�P���I��ڑO�ɂ��Đl�ނ̎��R�F���͋���ȑO�i�𐋂����̂ł��B
�@�@�@�@�@�@�@�@�@�@�i�����j�@�@�i����@�G�E�֓��w�@��w�u�t�������w�j�@�@���y�j�f��
private page��

 �@�@
�@�@

 �@�i�E�i�E�g���\�������������d�q�́A���̎��ʂƕ��̓d�ׂ������ĉ^����������q�ł����B�������ނ́A���ʂƓd�ׂ̔�����������̂́A���̎��͂��ꂻ��̒l��f��I�ɂ͎����܂���ł����B
�@�i�E�i�E�g���\�������������d�q�́A���̎��ʂƕ��̓d�ׂ������ĉ^����������q�ł����B�������ނ́A���ʂƓd�ׂ̔�����������̂́A���̎��͂��ꂻ��̒l��f��I�ɂ͎����܂���ł����B




 �@
�@















